Some notes on projective geometry

Projective geometry originated in the Renaissance when artists sought a method to introduce accurate perspective into art. This artistic perspective assumed that the viewer had a single, point eye and that the artist's canvas lay between the eye and the contents of the view. The problem of projective geometry then consisted of discovering how the relationships in the view would be transferred onto the canvas. Projective geometry allowed the creation of highly convincing pictures.


Canaletto - La Regata Vista da Ca' Foscari Courtesy Wikicommons


In ordinary projective geometry the eye, the plane of the canvas and the planes in the view are separated by the space along a line from the point eye to the objects in the view.


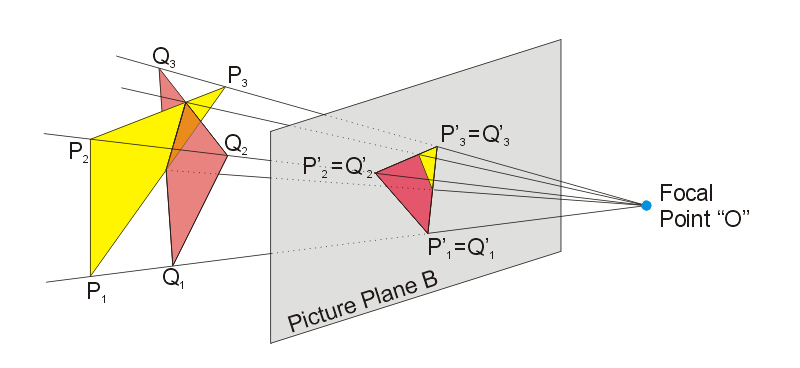
Principle of perspectiveCourtesy Wikicommons

There is an interesting guide to perspective in art at: Scribd: Projective Geometry and a good introduction to simple projective geometry at: Projective geometry by Tom Davis.


Until the twentieth century physicists regarded this geometry as little more than an interesting insight into perspective drawing although mathematicians such as Klein thought that it might lie at the root of all geometry. However, in 1908 Hermann Minkowski discovered that Einstein's theory of Special Relativity was actually due to the existence of four dimensional spacetime and could be analysed using projective geometry (See Silagadze 2007).

Einstein's Theory of Relativity is one of the most important discoveries of all time because it describes the world as four dimensional. According to relativity theory things can be arranged left-right, up-down, back-forwards and past-future.

Suppose you and I are together then you walk straight down the street for 3 metres and make a right angled turn to the left then carry on walking for 4 metres. How far away from me will you be "as the crow flies", or, to put it more technically, what is the relationship between 3 metres in the forward-back direction and 4 metres in the left-right direction?

Most older children know the answer to this question, the relationship is known as Pythagoras' Theorem and we all learnt Pythagoras' Theorem at school: in a right angled triangle the square on the hypoteneuse equals the sum of the squares on the other two sides. In my example 3 squared plus 4 squared is 9 + 16, or 25, and this is the square of the distance as the crow flies. So the distance as the crow flies is the square root of 25 or 5 metres. The same reasoning applies to you walking 3 metres away from me then climbing a 4 metre pole, you will again be 5 metres away as the crow flies. So up-down, forward-back and left-right directions are related to each other by Pythagoras' Theorem (h²=x²+y²).

But how are these three directions in space related to time?

How far away is something that is 4 metres away but also a second in the past? According to physicists this distance (called a space-time interval) is given by a modified version of Pythagoras' Theorem where the square of the space-time interval equals the square of the spatial distance MINUS the square of the distance in time - in maths: h²=x²-T². The distance in time is measured in metres and is related to the time in seconds by a constant, "c", which is numerically equal to the speed of light in a vacuum.

If you are not familiar with relativity this idea of things being separated from you by both time and space will be strange and may seem simply wrong. I would strongly recommend Wikibooks: Special Relativity as an introduction.

The immediate consequence of this interdependence of space and time is that only things that have a space-time interval of zero relative to you can be in contact with you now. All other things are separated from you by time or by space. This gives rise to the modern, physical idea of an observer as a point at the centre of all incoming and outgoing light rays because only things travelling at the speed of light can have a space-time interval of zero.

Those events that have a space-time interval of zero relative to an observation point can be represented by a geometrical form known as the "light cone". The diagram below shows a light cone.



Image courtesy of Wikibooks: Special Relativity.

When people first come across the "lightcone" they think that it is straightforward because information must be transmitted to us by photons or by lumps of matter actually hitting us. So, of course, it is obvious that the only things we can know are things that have a zero space-time distance from us. At first sight it seems that the light cone is about the delivery of photons and nothing else. However, when I was considering simple distances the hypotenuse was a real distance, it was shorter than walking along two sides of a triangle. If this is true then the space-time interval should actually be shorter than the combined distance travelled through space and time. So when we see a photon is its source right next to us because the space-time interval is zero or is the source separate from us? The answer to this question depends upon the reality of dimensional time.

Another consequence of the reality of time would be that when we move about each of us has a very slightly different set of things in what we regard as our "present instant". In other words, in a 4D universe, different events are simultaneous for different, moving observers.

This prediction of Relativity Theory theory is exposed in an exaggerated form in the "Rietdijk-Putnam-Penrose" argument. Penrose described the argument:

"Two people pass each other on the street; and according to one of the two people, an Andromedean space fleet has already set off on its journey, while to the other, the decision as to whether or not the journey will actually take place has not yet been made. How can there still be some uncertainty as to the outcome of that decision? If to either person the decision has already been made, then surely there cannot be any uncertainty. The launching of the space fleet is an inevitability." (Penrose 1989).



Image courtesy of Wikibooks: Special Relativity.

The important thing to remember about this argument is that it applies to things that occur in the hypothetical present moment at great distances from the two people. What the people actually see at any moment is the light that left Andromeda 2 million years ago and they both see near enough the same light when they are together. The light left Andromeda 2 million years ago and the burning question for our two observers is to guess what is happening now. It turns out that relativity predicts that each individual has different events in their distant present moments and this means that either time exists or we each live in our own fantasy world. Recently the existence of time has been confirmed by experiments that allow electrons to interfere with their own past selves.

Philosophers tend to recoil from this approach to the universe because it appears as if all events would be fixed forever and there would be no free will (See Is There an Alternative to the Block Universe View? Petkov 2007). Scientists, on the other hand, would suspect that there must be more to the universe than four dimensional space-time. Perhaps another direction for arranging things (a fifth dimension) or maybe quantum theory puts the variability into life.

What is interesting about relativity in the context of the philosophy of mind is that, if dimensional time exists, any set of events that lie on a light cone can be at no distance from the point at the centre of the cone. In effect the events can all be at a single point even though they are still separated in space and time. This possibility of events being "out there" in space and time but bridged together at a point is very similar to our empirical conscious experience. In other words, projective geometry gets really interesting when one of the directions for arranging things has a negative sign in Pythagoras' Theorem (what Hermann Weyl called a "negative dimension") - when negative dimensions are present there are paths, such as the paths of photons, that are measured to have zero length in the spatiotemporal direction of travel.


Introductory texts

Nineteenth Century Geometry. Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/geometry-19th/#ProGeo

Investigations in Projective Geometry. Dwayne Alvis and Wanda Naborshttp http://jwilson.coe.uga.edu/EMT669/Student.Folders/Alvis.Dwayne/instruct/iu.html

More advanced texts

Davis, T. Projective geometry. http://www.geometer.org/mathcircles/projective.pdf

Silagadze, Z.K. 2007 Relativity without tears. http://www.arxiv.org/pdf/0708.0929

Wolfram MathWorld Projective Geometry. http://mathworld.wolfram.com/ProjectiveGeometry.html

Projective Geometry http://www.cs.elte.hu/geometry/csikos/proj/proj.html